|
|
| Startseite | Sonnenuhr live | Kalenderrechnung | BASS Kalender | Begriffserklärungen | Impressum | Datenschutz |
Vortrag Gerhard Benna bei der Deutschen Gesellschaft für Chronometrie in Trier  Bild 2 / Man Sagt: Die Sonnenuhr lügt nicht oder anders gesagt, die Sonnenuhr geht immer richtig.
Und diese Redewendung werden wie uns heute zu nutze machen.
Die Zwei Formeln unten, die eigentlich eine Formel sind, werden uns dabei helfen, einen seit über 2000 Jahren bestehenden chronologischen Irrtum zu klären.
|
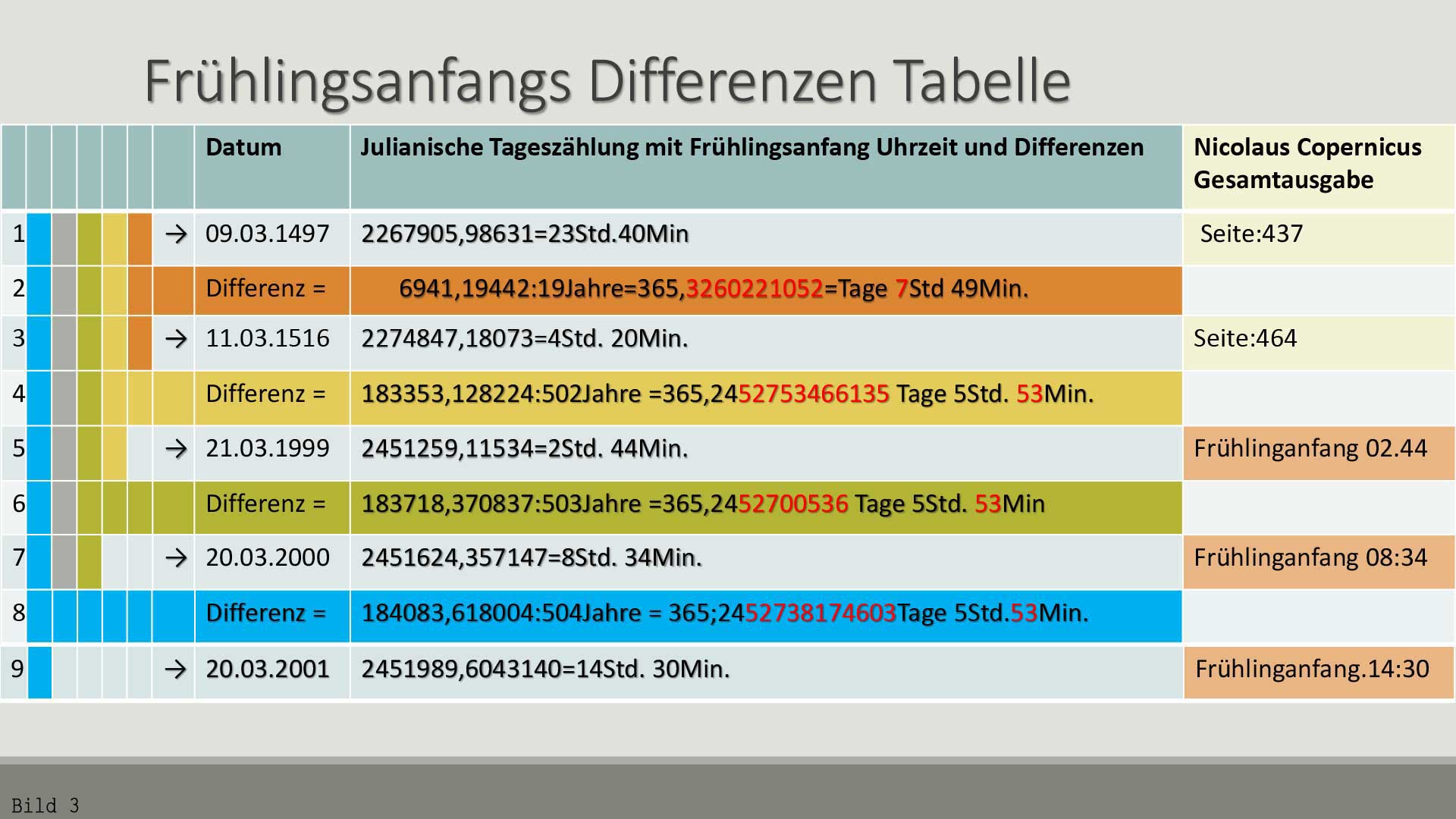 Bild 3 / Wir fangen mit Nicolaus Copernicus an. Pos. 2 ist die Differenz aus Pos.1 und Pos.3. Gleiches gilt für Pos. 1 und 5 die Position 4 ergeben. Und nach dem gleichen Muster geht es weiter. 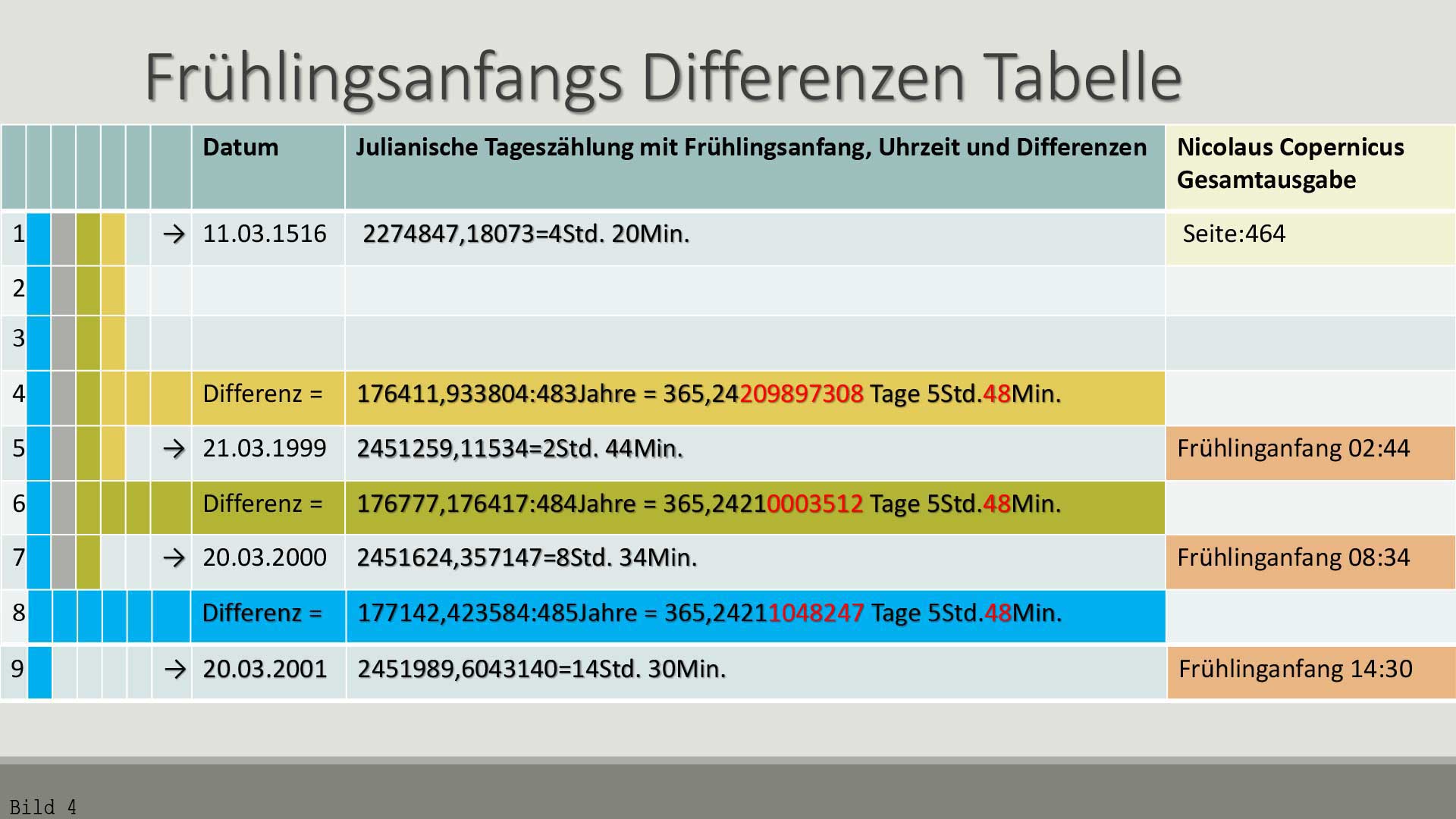 Bild 4 /
Hier vergleichen wir den Frühlinganfang von 11.03.1516 wieder mit dem Frühlinganfang von 1999/2000/2001.
Es ist deutlich zu sehen, dass die drei Differenzwerte nicht weit entfernt vom heutigen wissenschaftlich errechneten Wert des tropischer Jahres von 365,24219 Tage sind.
|
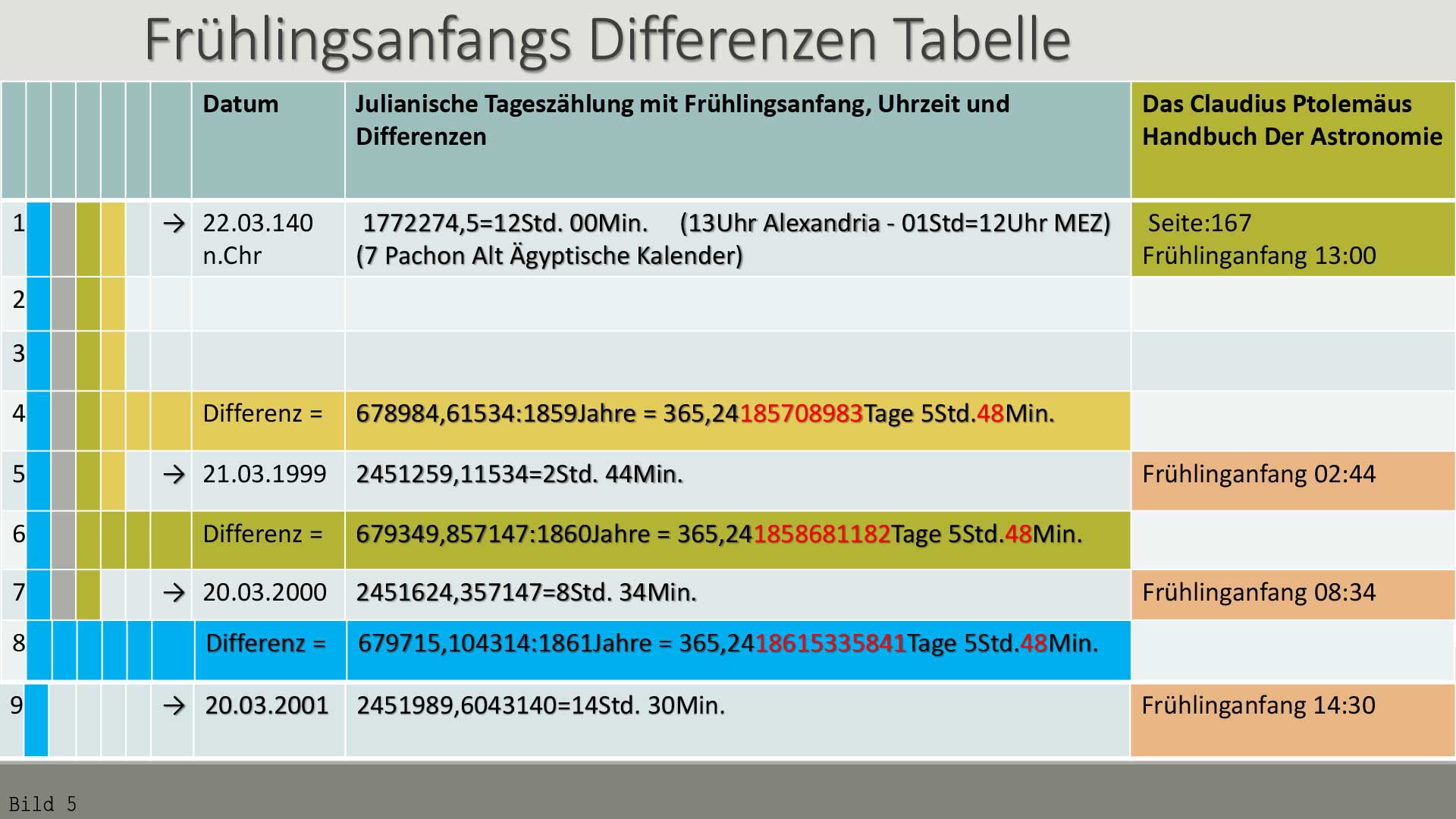
Bild 5 / Jetzt gehen wir zu den Frühlingsanfangsdaten des Claudius Ptolemäus.
22.03.140 n.Chr ist auch 7.Pachon des Alt Ägyptischen Kalenders, was sehr wichtig ist. Wie bei der letzten Folie: Ein Tropisches Jahr ist 365 Tage 5 Stunden 48 Minuten 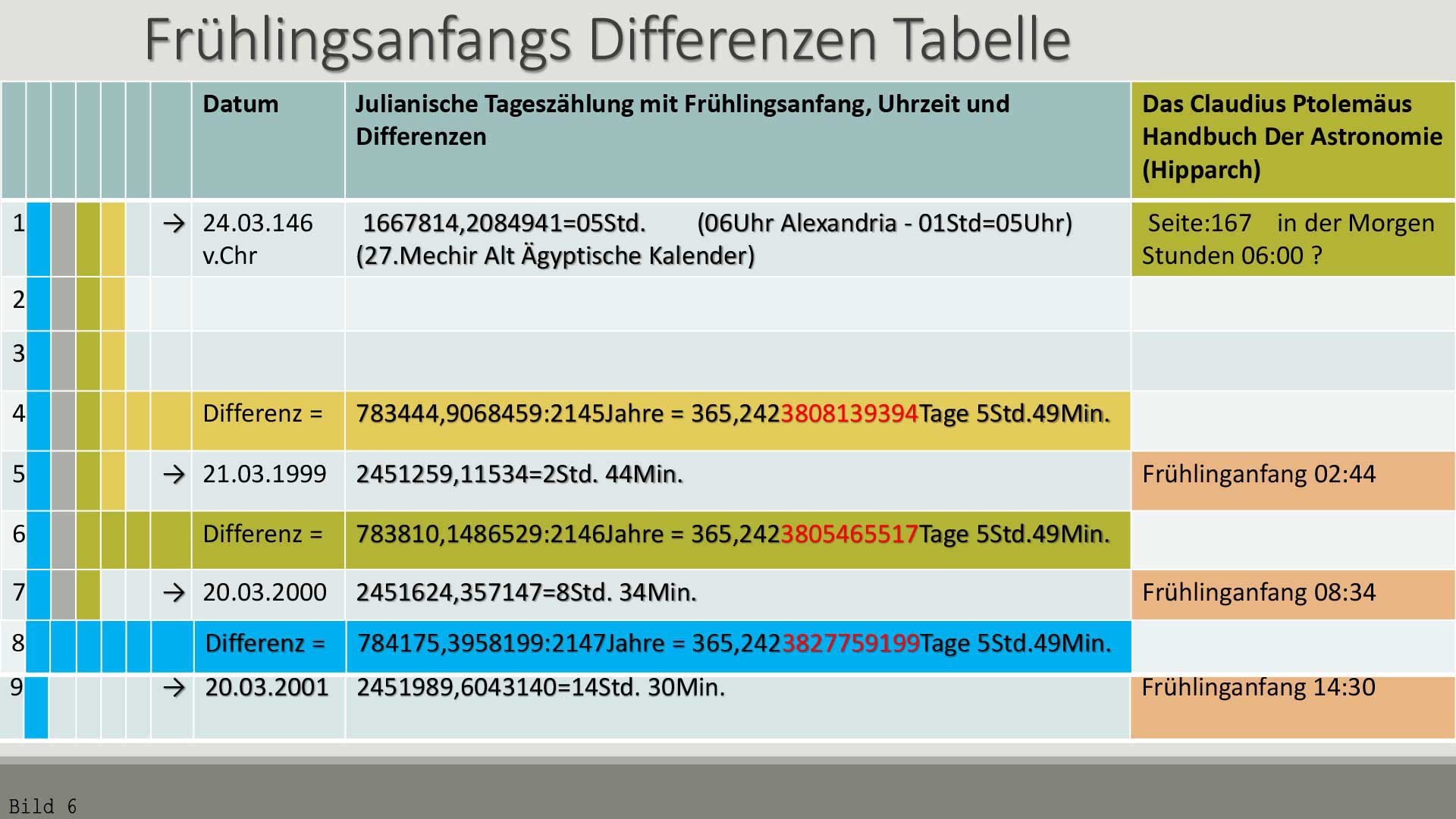 Bild 6 / Hier sind wir bei Hipparch' Frühlinganfang.
Jetzt haben wir einen Durchschnittswert des Tropischen Jahres: 365Tage 5Stunden 49Minuten Das ist auch einer von vielen Gründen dafür, dass unser Tropisches Jahr heute den Wert 356 Tage 5Stunden und 49 Minuten hat. |
 Bild 7 / Hier muss ich staunen: Wie ist das möglich? Vom 20.03.2000 bis 20.03.2001 beträgt der Tropisches Jahr Wert 365 Tage, 5 Stunden und 55 Minuten. 6 Minuten länger als der wissenschaftlich errechnete Durchschnittswert hier oben rechts zu sehen.  Bild 8 / Hier addieren wir zu Ptolemäus Frühlinganfangsdaten 14235Tage. Das ergibt 38,97 Jahre. Also nicht volle 39 Jahre, jedenfalls nicht bei der Verwendung von C. Ptoleämus Daten. Obwohl es um diese Uhrzeit noch dunkel wahr, hat er behauptet, selbst den Frühlinganfang zu beobachten. Also, hat er den Frühlingsanfang nur berechnet. Weil die Daten des Frühlinganfangs das Fundament jedes Kalenders sind, ist aus falschen Daten und falschen Entscheidungen ein falscher Kalender entstanden. |
 Bild 9 / Nächste Kategorie: Die Sonnenuhr als Messgerät: Zuerst möchte ich Ihnen die Funktion des Sonnenuhr-Kalenders ein bisschen erläutern.
Wir beschäftigen uns heute aber nur mit den Daten des Frühlingsanfangs.  Bild 10 / Hier beziehe ich mich wieder auf C. Ptolemäus.
Zum 24.03.146v.Chr addieren wir auch die 14235 Tage aus vorletzter Folie und kommen auf 14.03.107 v.Chr oder auch 27 Mechir. Dieses mal aber verwenden wir den fast identischen Wert des Tropischen Jahres von C. Ptolemäus: 365,2466374269006 Tage. Im Buch von Ptolemäus steht geschrieben, dass der Frühlingsanfang in der Morgen Stunden stattfand. Nach meiner Meinung in Alexandria 3:46 wenn 2:46 MEZ war. |
 Bild 11 /
So ist die dicke Tag- und Nachtgleiche-Linie am 20.03.2019 entstanden. Nach unseren Berechnungen ist aber Frühlinganfang um 5:16, wie man unten sieht. 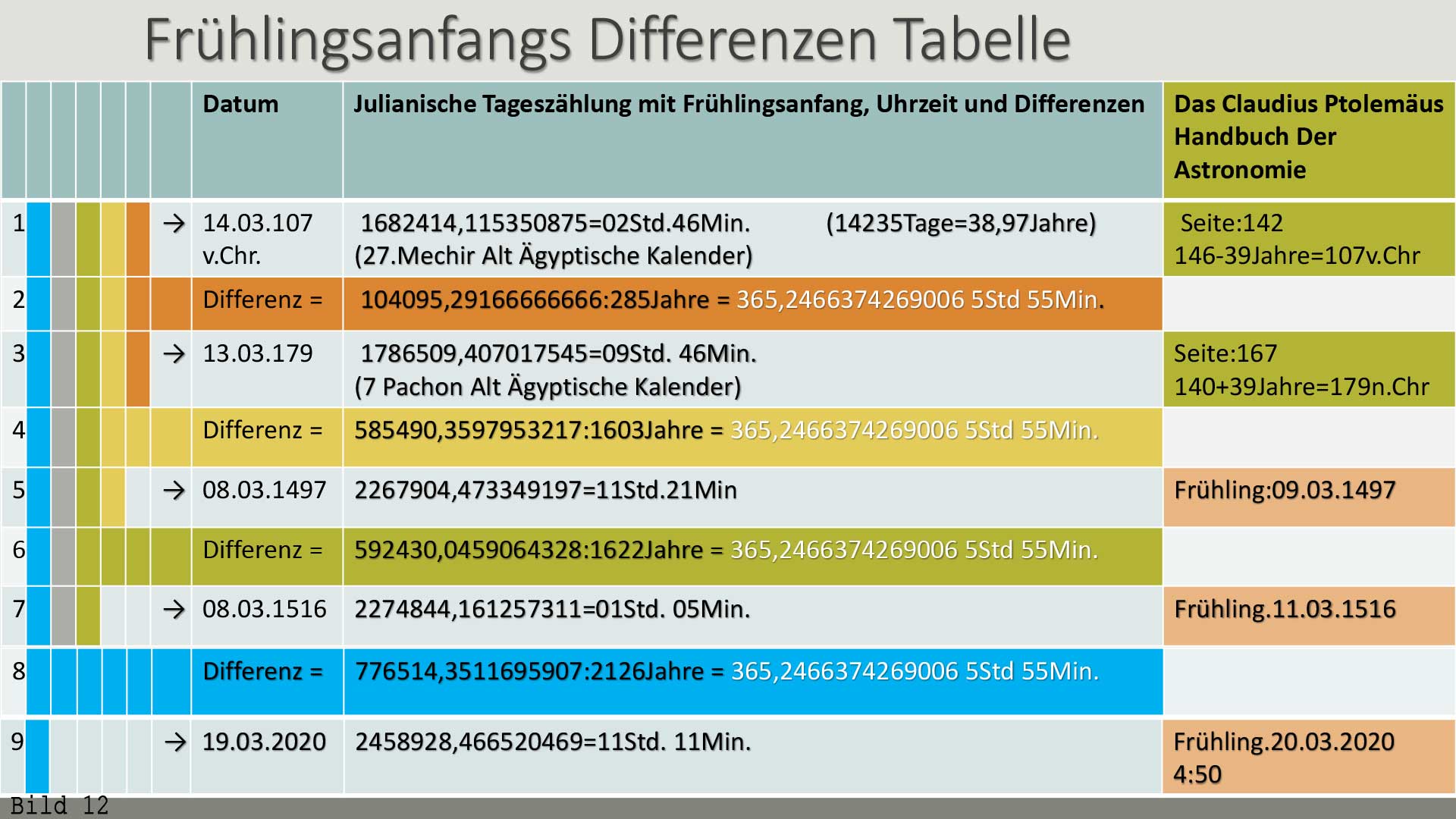
Bild 12
/ In den nächsten Folien werden wir mehrmals nur die Werte von Position 8 und 9 ändern - bezogen auf Position 1. Zwischendurch zeige ich immer wieder ein Bild der
Sonnenuhr mit Beschreibung dazu.
|
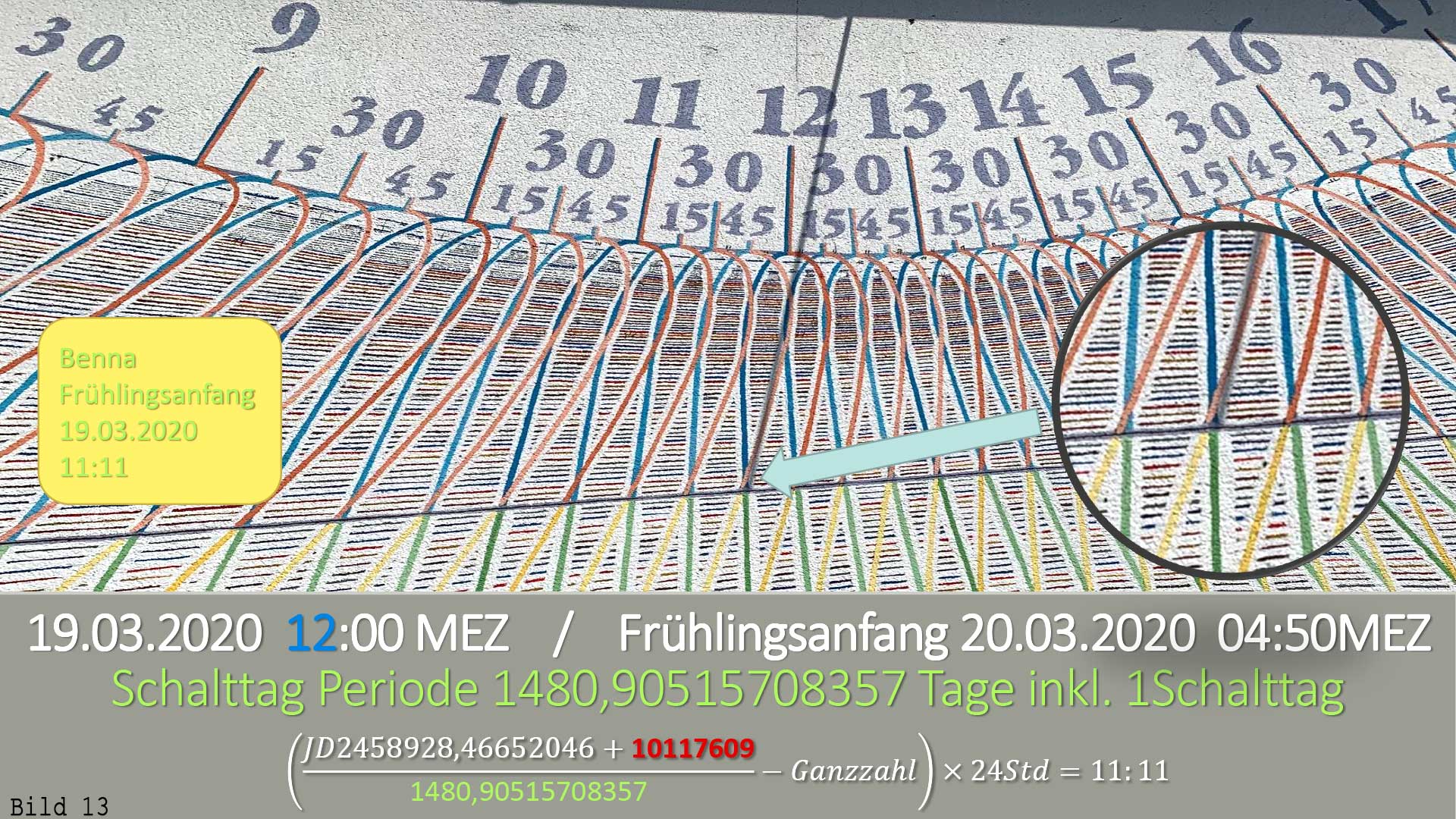 Bild 13 /
An diesem Tag 19.03.2020 ist der Frühlingsanfang um 11:11 Uhr, und nicht am 20.03.2020 um 4:50 Die Sonnenuhr geht immer Richtig, Oder?  Bild 14 / 19.03.2021 ist genau das Gleiche (wie vor).
|
 Bild 15 /
Schon wieder ist am 19.03.2021 der Frühlingsanfang und nicht am 20.03.2021  Bild 16 / Und wieder ist am 19.03. Frühlinganfang, dieses mal um 23:02 im Jahr 2022 |
 Bild 17 /
Obwohl dieses Bild am 20.03.2022 um 16.30 gemacht worden ist, sehen wir, dass der Schatten ein Strich weiter ist, als er eigentlich sein sollte.
Damit stellen wir fest, dass der Frühlinganfang am 19.03.2022 sein muss, wie unten bei der Formel zu sehen ist. 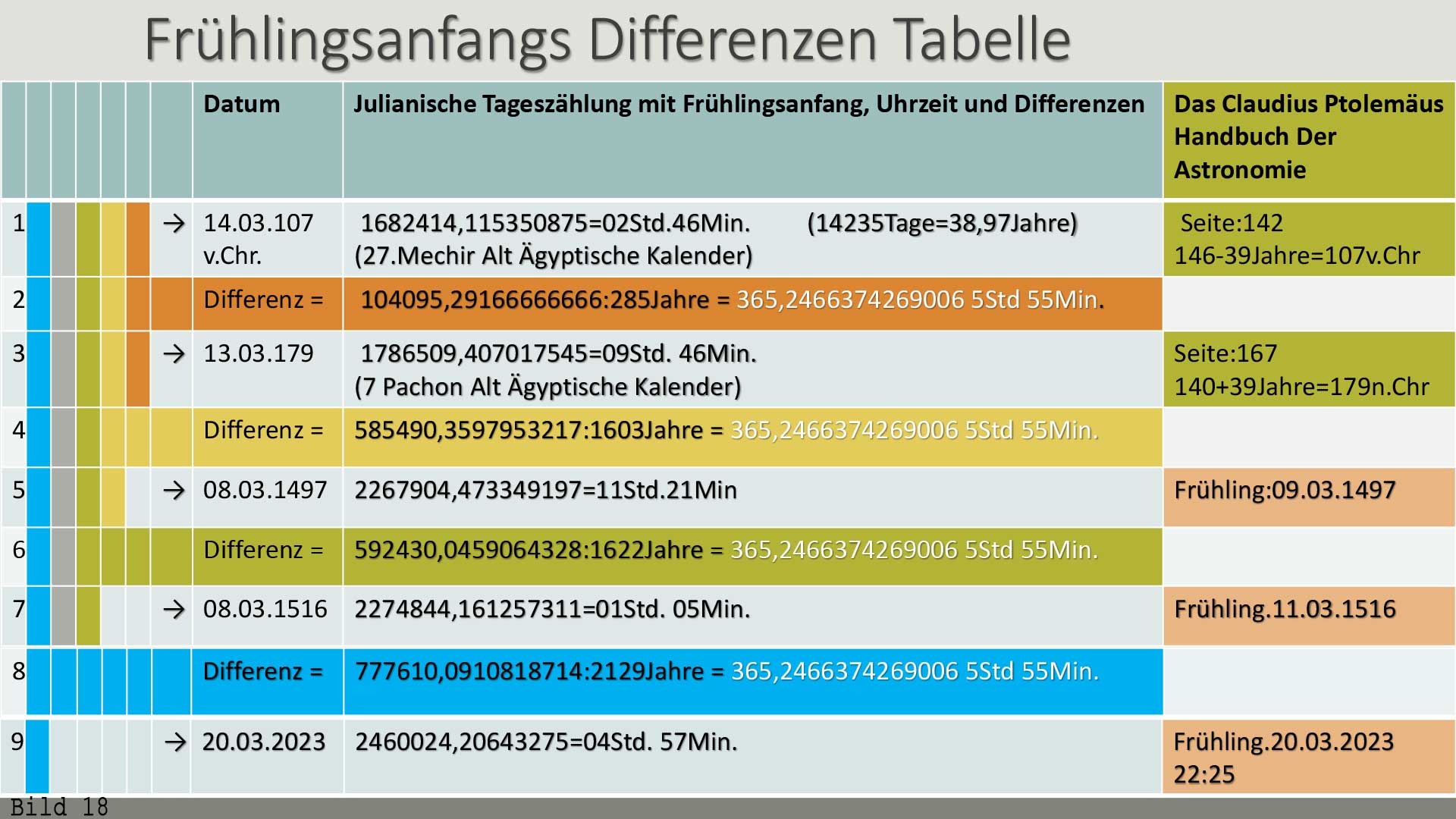 Bild 18 /
2023 war Frühling tatsächlich am 20.03 nur zirka 12 Stunden früher als der wissenschaftlich errechnete Frühlingsanfang.
|
 Bild 19 /
Hier sehen wir, dass das Schattenende ein Strich früher ist als der Frühlinganfangsstrich,
weil das Bild am 19.03.2023 entstanden ist.  Bild 20 /
Und nun sind wir schon im Jahr 2024 angekommen. Weil aber am Frühlinganfang die Sonne in Atzenhain nicht geschienen hat, wird hierfür ein Bild vom 17.03 als Nachweis verwendet.
|
 Bild 21 /
Und so sieht das aus: wir brauchen nur zwei Striche dazu zählen und wir kommen wieder auf den 19.03.2024 um 10:51

Bild 22 / Um die Position des Objektes am Himmel festzustellen, addieren wir zum Julianischen Datum immer den festen Wert von 10117609 Tagen dazu. Dieses Ergebnis dividieren wir durch den periodischen Umlauf des Objektes. Nun subtrahieren wir die Ganzzahl des Zwischenergebnisses, also die Zahl vor dem Komma. Das Ergebnis, das nach dem Komma bleibt, multiplizieren wir mit 360°, so bekommen wir die Position.
Oder wir multiplizieren mit 24 Stunden und bekommen dann die Uhrzeit. |
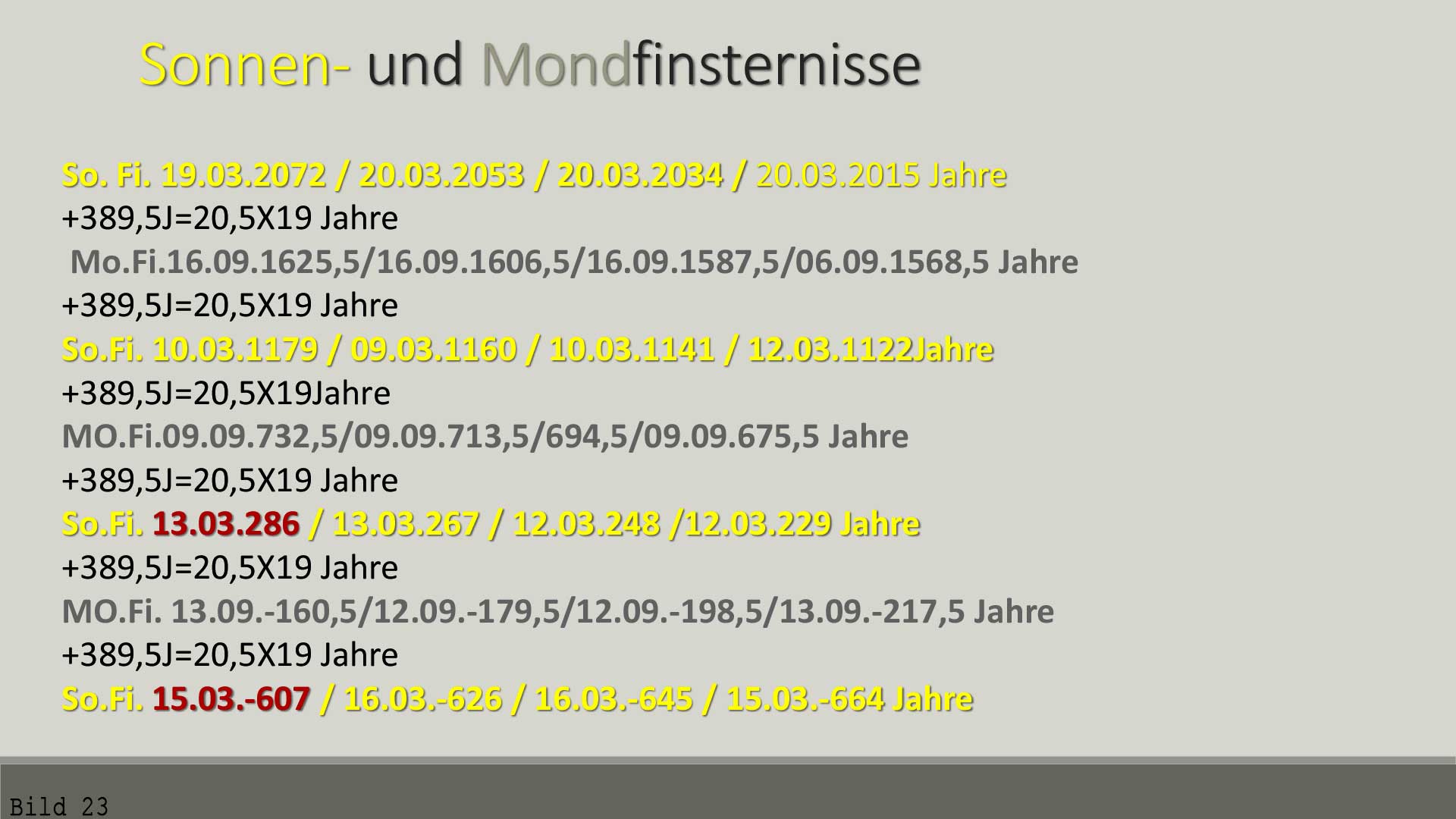 Bild 23 /
Nächster Abschnitt: Sonnenfinsternisse, die auch am Frühlingsanfang stattgefunden haben sind
gelb markiert. Grau markiert sind Mondfinsternisse die 5 Tage vor dem Herbstanfang stattgefunden haben. Die Sonnenfinsternisse sind in 4x19 zusammengefasst, was auch Kalipische Periode genannt wird. Der Abstand von Kalipischer Periode zur nächsten Kalipischen Periode sind genau 893 Jahre, was 326165,24722222222Tagen entspricht. Das heißt, das Jahr 2015-893 Jahre ist das Jahr 1122 n.Chr 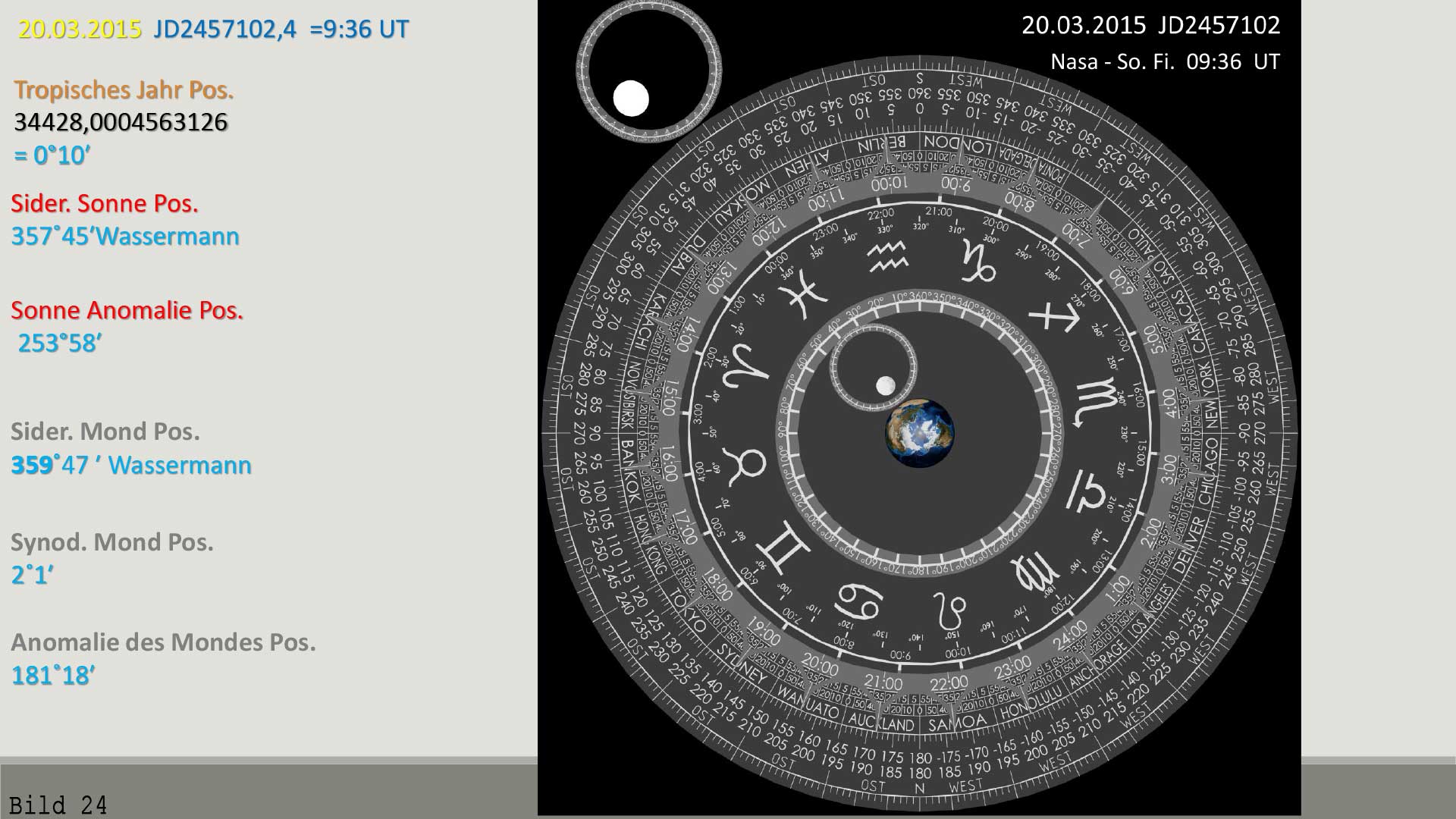
Bild 24 / An diese Sonnenfinsternis am 20.03.2015 n.Chr zu Frühlingsanfang können sich einige bestimmt noch erinnern.
Wie bei C. Ptolemäus, verwenden wir eine geozentrische Bewegung. Nur eine kreisförmige Bewegung mit Epizykel. |
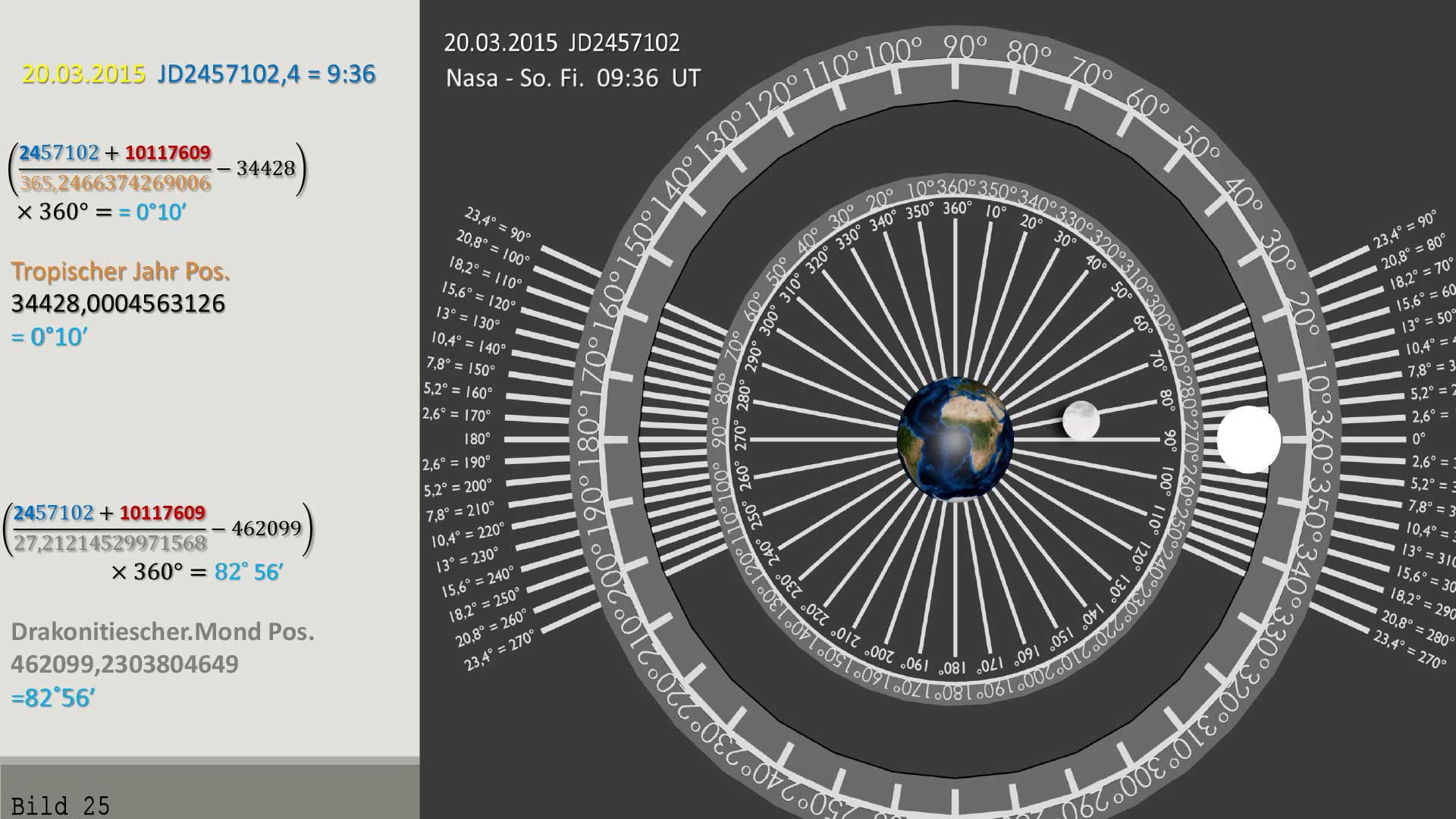 Bild 25 /
Geozentrische Ansicht – seitlich 20.03.2015 n.Chr
 Bild 26 / Genau 893 Jahre früher ist das Jahr 1122 n.Chr
|
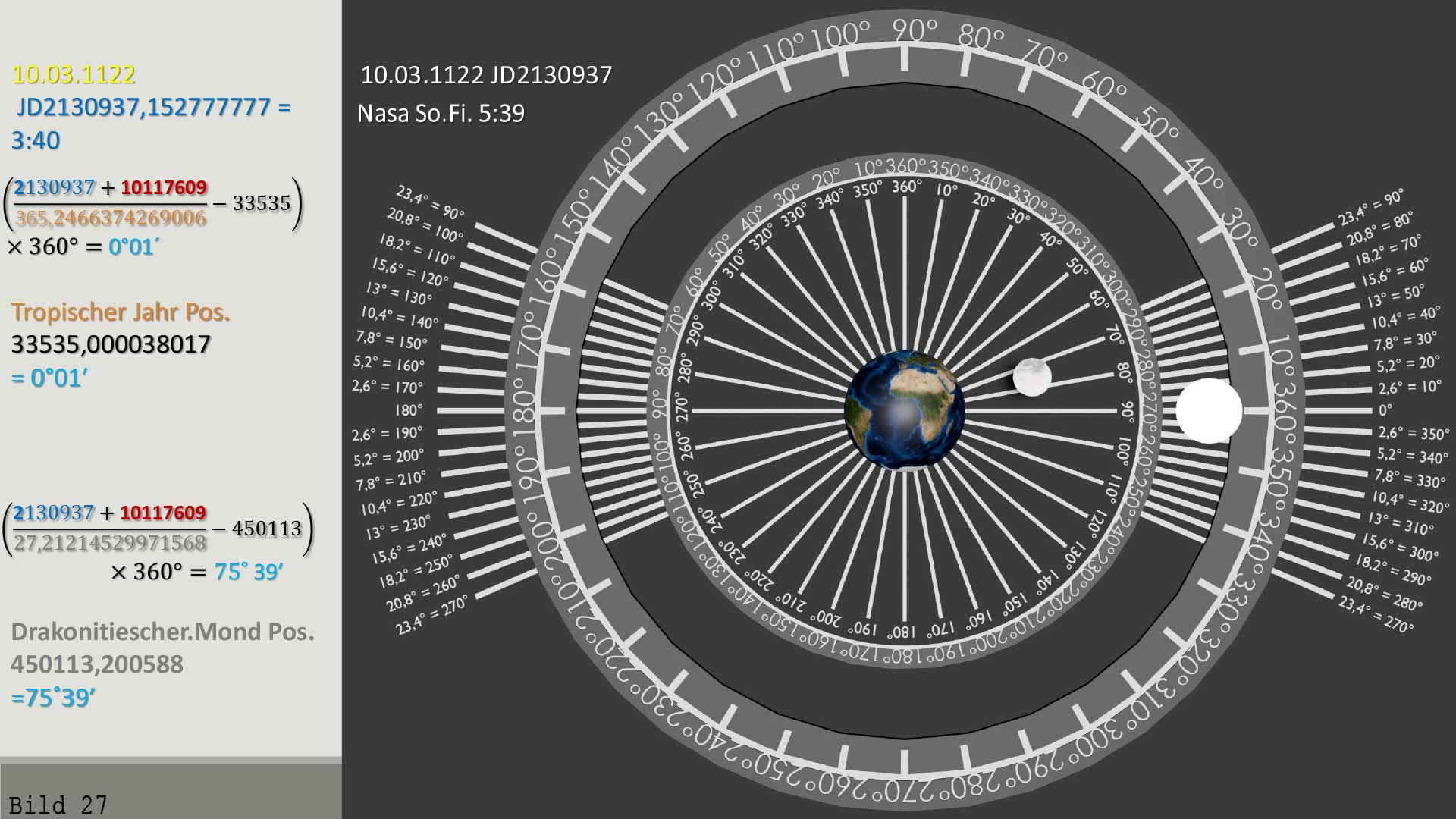 Bild 27 /
Geozentrische Ansicht – seitlich 1122 n.Chr
 Bild 28 / Und noch mal 893 Jahre weiter.
Zurück ist das Jahr 229 n.Chr |
 Bild 29 /
Gleiches Jahr 229 n.Chr - nur seitliche Ansicht.
 Bild 30 / Von 2015 n.Chr bis 664 v.Chr sind 3 x 893Jahre, das sind 2679 Jahre oder 978495,7416666666 Tage.
Dies entspricht 978495 Tage, 17 Stunden, 48 Minuten. |
 |
|
|
|
|
|
|
|
|
|
|